Operators

Previously we saw that we can store information in objects called variables. It is logical to assume that if we can store some information, there must be some way to manipulate the mentioned, other than printing it. Manipulation of data is done through operators.
The basic arithmetic operations are available in C++, but with a slight caveat. We need to watch out for upon which data types are we performing these operations. Taking this into consideration, we will explain every operator for each data type separately.
 
Let’s start with integers. The basic arithmetic operations are the same as in math except for one, division.
int a = 3;
int b = 4;
int c = a + b; // c = 7
int d = 2 * a - b; // d = 2
int e = c / d; // e = 3
Every single arithmetic operation excluding division when done on integers must have a result that is an integer and we know that from math. The tricky part is division. In the example given, dividing 7 by 2 should give us a rational number, 3.5 to be exact. Engineering have thought long and hard what to do with division and came up with a solution – whole division. The procedure is simple:
  • If the result of dividing two integers is an integer, return that result
  • If the result of dividing two integers is a rational, return the closest integer smaller than the rational
If this confuses you a bit, you can think of it this way: If two numbers when divided return a rational, just cut off the numbers after the dot and that is your result.
Additionally, in C++ there are special operators which use addition and subtraction. The first kind of operators are increments and decrements. They are essentially operators which take the value of the variable, increment/decrement it and then store the newly formed value back in the variable. When it comes to these operators, there are two kinds of them:
  • Pre-increment and pre-decrement(++var and –var)
  • Post-increment and post-decrement(var++ and var–)
The first pair of operators work in the following way: Firstly the operation will be done and the the newly formed value will be used. The second pair works differently: Firstly the old value will be used and then the post operation will be applied.
int a = 3;
int b = a++; // b = 3 and a = 4
int c = --a; // a is firstly decremented; a = 3, then its assigned to c; c = 3
int d = --a + b++ + c--; /* a = 2; b's and c's old values are used while calculating d
because of the post increment/decrement (b = 3; c = 3;). d = 8; After the value is stored in d,
b and c are incremented, decremented respectively*/

Finally, there are special type of operations which are a combination of arithmetic operators and the assignment operator. The functionality of those operators is to do the supplied operation with the old value of the variable on the left and the expression evaluated on the right and to assign the newly formed result to the variable on the left:

int a = 1;
int b = 2; 
int b += a; // Equivalent to b = b + a; b = 3
a -= a - b; // a = a - (a - b); a = 3
int c = 6;
c /= a + b; // c = c / (a + b); c = 1
c *= c + a * b; // c = c * (c + a * b); c = 10

One additional operation you have when dealing with integers is the modulo (denoted as “%“). The result of this operation represents the remainder of division.

int a = 38;
int b = a % 3; // 38 / 3 = 12 with remainder 2. So b = 2

int x = 3;
int y = x % 2; // 3 / 2 = 1 with remainder 1. So y = 1

a %= (x+y)*b; // Equivalent to a = a % ((x + y) * b); a = 6

When it comes to floating point numbers, everything is the same as in math. Here we don’t have a problem with division because dividing two rational numbers is bound to give us a rational, which can be represented by a floating point data type.

float x = 3.1;
float y = 2.0;
float a = x + y; // a = 5.1
a = x * y; // a = 6.2
a = 2 * x / y; // a = 3.1

Finally, one of the most useful operators you might use when doing any complicated calculation is the bracket operator. It works the same way as in math. Its functionality is to group the order of operations which are being evaluated in your expression.

int a = 2 + 5 * 3; // 17
int b = (2 + 5) * 3; // 21

Binary

You may have heard somewhere that a computer works and communicates through something called binary. Even though the word itself was popularized by movies and TV shows for being something complex and technical, it is actually rather simple. When we think of numbers, we think of a sequence of digits, where each digits ranges from 0 to 9. That way of representing numbers is called the decimal system. This number system seems natural to us because we have been surrounded by it our whole lives, but when we change to a new number system, it may be difficult in the beginning. If you think about it, a number system just tells us the amount of information we can store in a single entity. That entity in this case is a digit. It would be logical to assume that the simplest number system we can have is consisted out of entities that have something or not, that are true or false, that are 1 or 0. This is where the binary system comes into play. The whole logic is that every digit is either a 1 or a 0. So how do we represent our numbers in the binary system? The procedure is given below.
 
Every digit has its positional weight in the binary system. Let’s look at the picture below:
binary_redefined
We read digits from right to left. That means that the far right digit has weight of 2^0, the one next to him (to the left) has weight of 2^1 and so on.
How do we then represent our binary number into the decimal system? Every digit (0 or 1) will be multiplied with its own weight and then all of the results should be added to get the decimal representation of our binary number. In our case, the procedure is as follows:
0*(2^0) + 1*(2^1) + 0*(2^2) + 1*(2^3) = 0 + 2 + 0 + 8 = 10
So, our binary number is actually a decimal number 10.
That’s easy, right?
 
Now let’s look at how we can represent a decimal number 10 as a binary number. The procedure is as follows:
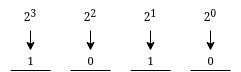
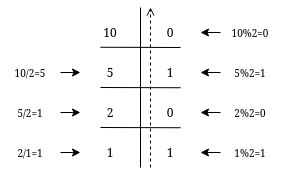
  • At the top of the left column, put the number you want to represent in the binary system (10 in our case)
  • Calculate the modulo of that number with 2 and put it next to it in the right column
  • Calculate the integer quotient (whole division) of that number with 2 and put it below it in the same column (left)
  • Repeat the process for every row until you get 1 in the left column
  • The binary number is read from the right column, from the bottom to the top
decimal_to_binary_redefined
Let’s read our binary number from the bottom of the right column, to the top right: 1010 and that is the binary representation of a decimal number 10.
Exercise: What number might this be: 101001110? Comment down below the number you got.

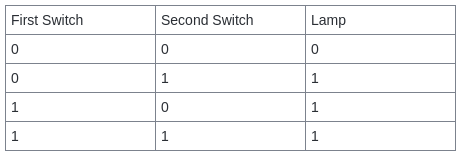
Binary logical operation

You may have heard a term used in computer science called Boolean algebra. It simply denotes a set which has only two elements, binary 1 and 0, and a couple of operations we can do with 1 and 0. Those operations are widely known as logical operations.
The reason why they are called like that is the fact that if you make an analogy, where 0 is the off state of something (for example a switch) and 1 is the on state, the logical operations would denote a combination of multiple states which can be either a 1 or a 0
Let’s look at an example.
Imagine that in your living room there is a lamp. The lamp is controlled by two switches. The way you turn on your lamp is by flicking either of the switches. But if you want to turn it off, you need both of the switches to be off. We can represent the switches and the lamp in a table:
table1 (1)
With 0, we have represented if the switch/lamp is off and with 1 if the switch/lamp is on. The table above is also called a truth table and the operation where we have two variables (first switch and second switch) and an output variable (lamp) is called an or operation. The name is quite intuitive: “If the first switch or the second switch is on, the lamp is on”. The or operation is also sometimes denoted as “+” or as “|“.
There is also an operation called and, and is sometimes denoted as “*” or as “&“. Its truth table is given below:
table2
z = x * y ➝ If both x and y are on, so is z.
The last operation we need to look at is the not. Not simply turns 1 into a 0 and 0 into a 1.
 
Lastly, a small point regarding convention. In computer science and engineering in general, single digits in the binary system are called bits. A group of 8 bits is called a byte.

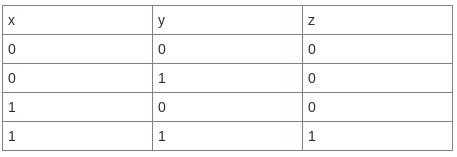
Logical and bitwise operators operators in C++

In C++, there are two types of operators which have boolean logic implemented in them:
  • Logical operators
  • Bitwise operators
Logical operators are operators which resemble the operations we have seen with binary numbers. The operands of the logical operators are considered to be boolean and in the same way operations with binary numbers work, here they are done on booleans( true representing 1 and false representing 0).
  • And operator – represented as “&&“. If both operands are true, it returns true.
  • Or operator – represented as “||“. If either operand is true, it returns true.
  • Equals operator – represented as “==“. If both operands have the same value, it returns true. This works for any primitive data type
  • Not equals operator – represented as “!=“. Has the opposite functionality of the equals operator
bool first_condition = (true && false) == (false || true); // You figure it out Einstein
bool last_condition = first_condition != true;
Lastly, bitwise operators are operators which perform logical operation on each pair of bits from the pair of variables, respectively. This is done in the background in the following way:
  • The pair of variables get transformed into their binary representation
  • Next, each pair of bits starting from the right of each variable is used in the operation
  • The bit operation gets evaluated and stored in the result in the same position as the position of the bits in the pair of variables.
  • Every pair of bits then gets evaluated in the same fashion and the resulting value gets transformed from its binary representation into the adequate data type.
To make this easier to understand, let’s first look at how we can assign binary values to our regular variables of the known data type. In C++, if we want to assign a binary value, in front of the binary value we put “0b” and then the actual value right after it. Here are some examples:
int x = 0b1011; //Binary representation of the decimal number 11 assigned to an integer
int y = x + 0b01; /* y is assigned the value x plus the binary representation of the number 1;
y = 12;*/
Now that we know how to represent binary numbers in C++, let’s look at the bitwise operators. The following list contains bitwise operators in C++:
  • And (&)
  • Or (|)
  • Shift left, shift right (<< and >>)
  • Xor (^)
And, or and not we already know from learning about binary numbers, but the key difference here is that the operation are done on each pair of bits from the pair of variables respectively.
int x = 0b0001;
int y = 0b0010;
int c = x & y; // c = 0b0000
int d = x | y; // d = 0b0011

Shifting represents an operation of moving the bits to the left or to the right of the first operand by a value defined as the second operand. The whole process is actually multiplying the first operand by a power of 2 defined by the second operand (shift left) or dividing the first operand by a power of 2 defined by the second operand (shift right).

int x = 3;
int y = x << 2; // y = 12
int z = y >> 1; // z = 6

Lastly, there is the xor operation. It is similar to and and or, but has a different way of working with the bits. The xor operation takes each pair of bits and if they are of the same value, gives the result 0. If the bits are different, it gives the result 1.

int a = 0b011; //a = 3
int b = 0b101; //b = 5
int x = a ^ b; // x = 0b110; x = 6
Next Lecture

Table of contents

Leave a Reply